|
Results |
|
II. – Low Density Low density
simulations were run for comparison to the high density cases. These simulations
yielded interesting results by themselves.
Figure
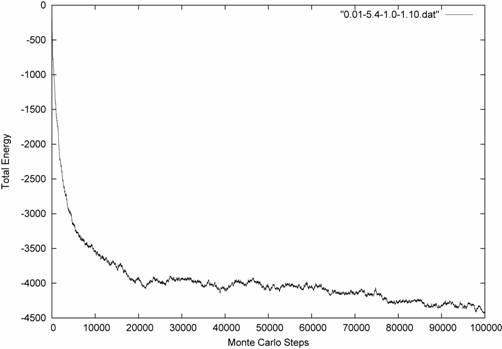
14. – Energy trace for a packing fraction of 0.01, energy of attraction and
repulsion of 5.4, ratio of 1.0, and an potential range of 0.1.
Figure
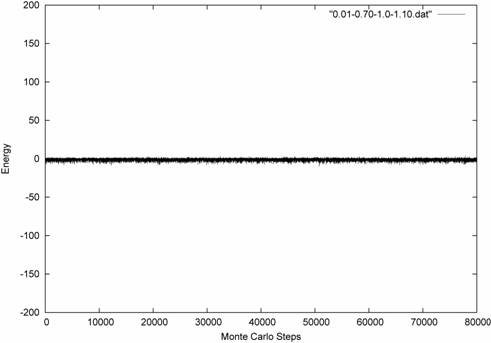
15. – Energy trace for a packing fraction of 0.01, energy of attraction and
repulsion of 0.7, ratio of 1.0, and an potential range of 0.1. From figure 14
it is evident that that run was not fully equilibrated but appears to be
leveling off as did the high density trace shown previously. The lower energy
situation in figure 15 almost equilibrates immediately and suggests at low
density and weak attractions very few aggregates form (a few dimmers). Screenshots of
our system near the equilibration point are shown for various conditions as
figures 16, 19, and 20.
Figure
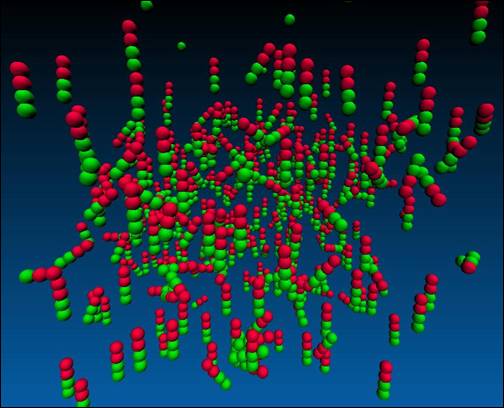
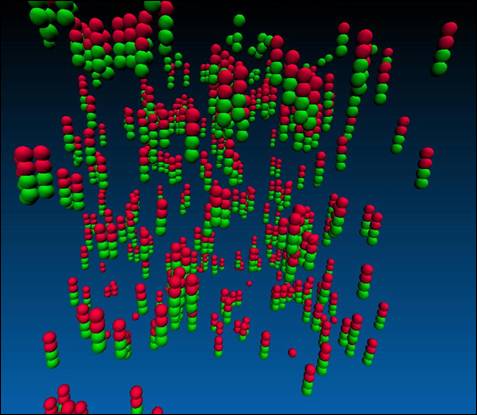
16. – System at a packing fraction of 0.01, attraction/repulsion energy of
5.4, ratio of 1.0, and an attractive range of 0.1. Figure 16 shows
some interesting features in the initial equilibration period as shown in
figures 17 and 18. The system was started anti-parallel as shown in figure
17, and roughly half of the rods re-orient (figure 18) so as to have a net
parallel alignment as shown in figure 16.
Figure
17. – Anti-parallel initialization (actually a few steps have already been
performed) for the simulation in figure 16.
Figure
18. – Very rapid re-orientation of the rods for the system in figure 16.
Figure
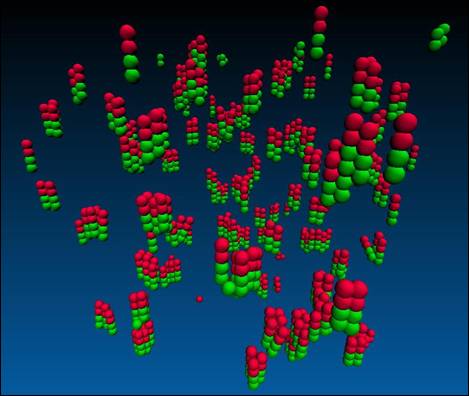
19. – System at a packing fraction of 0.01, attraction/repulsion energy of
2.7, ratio of 1.0, and an attractive range of 0.1.
Figure
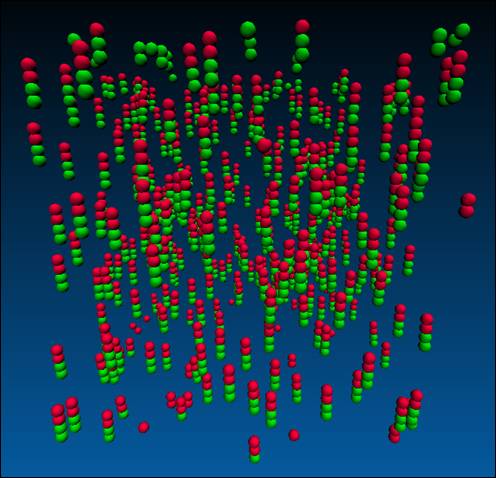
20. – System at a packing fraction of 0.01, attraction/repulsion energy of
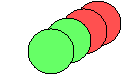
0.7, ratio of 1.0, and an attractive range of 0.1. It is evident
from the above simulations that a net alignment is favored with like ends
pointing in the same direction. As the attractive/repulsive energy is
increased discreet aggregation is observed; however, by intuition you would
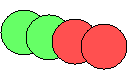
not expect this type of aggregation. The obvious guess at the aggregated
structure would involve greens clustering with the red tails as far away as
possible from one another. Care should be
noted that the liquid crystalline like structure may only be on a very local
scale and long range order may not be present. Larger simulations need to be
run to determine the range of this ordering if possible. The presence of
a nematic like phase at these low densities is, seemingly, very strange. One
potential rationalization is base off of an effective packing fraction
argument. Envision a sphere that encompasses the rod such that the rod is the
spheres diameter. Replace all the rods with spheres in the system and if the
spheres overlap rod geometry may play a large role and ordering may be favorable;
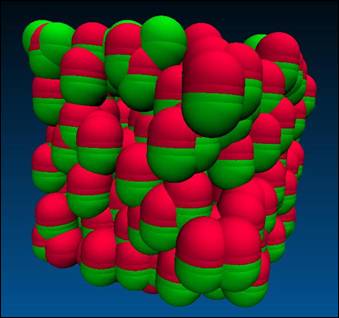
this argument can be seen in figure 21 where the particles have been blown up
to look more like effective, slightly elongated, spheres.
Figure
21. – Effective sphere model based off of the length of the rods as the
sphere diameter for the dilute rods cases. Figure 21
demonstrated that the system in figure 20 is actually quite dense when
considering the effective packing fraction which governs when rods begin to
overlap. The geometry argument sounds OK for the dilute weakly attractive
case but does little to rationalize the situations realized in dilute but
very attractive and all concentrated variations. Go To: High Density Results |