Modeling a Shaken Drop

Because the behavior of fluids can be quite complicated, it is often advantageous to create a simplified model. In order to better understand the behavior of the drops in their experiment, Noblin, Koffman, and Celestini developed a model that is a mechanical analog of the drop. 

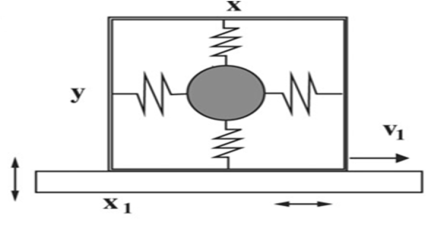
Noblin, Kofman, and Celestini’s model of a shaken drop as a mass on springs within a box that can slide on a surface. Courtesy X. Noblin, et. al.

In their model, they used a box containing a mass held by pairs of horizontal and vertical springs to represent the drop. When the surface on which the box rests is shaken, the mass can vibrate within the box (much like a liquid drop deforming in response to vibration), and the box itself can slide along the vibrating surface if the driving force is great enough to overcome the friction between the box and the surface (analogous to a liquid drop moving along a surface). Varying the stiffness of the springs changes the frequency with which the drop vibrates and the energy dissipated by this vibration., which in turn affects whether the box moves forwards, backwards, or remains in place.

Equations describing relationship between the difference in the frequencies of vibration of the platform in the horizontal and vertical directions are then fairly simple to write. Noblin, Koffman, and Celestini then used these differential equations to perform numerical simulations of how the box would behave under circumstances that most closely mirror those that would be found in the experiment.

 

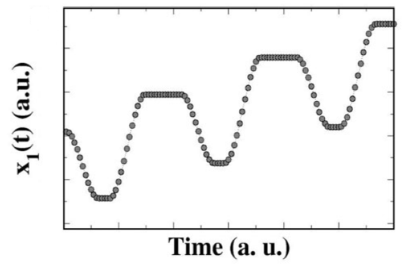The model displays characteristic ratchet-like motion and explains climbing drops.

The box moves forward a distance, pauses, then moves backward a shorter distance, pauses, and moves forward again. So even this extremely simplified mechanical model is able to produce the non-symmetric driving forces that allow the drop to travel in response to vertical vibrations. In addition, the equations can be adjusted to account for an inclined surface like that found in Brunet, Eggers and Deegan’s experiments, and this model accounts offers an explanation for the climbing drops they observed.

 

Photographs from Brunet and Egger’s experiment, showing an overhead view of a drop as it climbs an inclined substrate. Courtesy Brunet, Eggers and Deegan

Graph displaying the results of modeling, in which ratchet-like motion is clearly visible. Courtesy X. Noblin, et. al.

 

 

Some aspects of drop behavior remain unexplained.  When researchers looked at the relationship between the velocity of the box and the phase difference between horizontal and vertical vibrations, they found only one velocity maximum, a stark departure from the two maxima found when carrying out experiments on actual drops. More sophisticated models must be developed that can more accurately replicate this behavior.